How Slot Machines Work, casino slot machine winning percentage.

Casino slot machine winning percentage

New casino sites to play real money

When you hit the slot machines in a casino, you'll have dozens of gaming options. Machines come with varying numbers of reels, for example, and many have multiple pay lines. Machines don't loosen up on their own either. That is, they aren't more likely to pay the longer you play. Since the computer always pulls up new random numbers, you have exactly the same chance of hitting the jackpot every single time you pull the handle. The idea that a machine can be "ready to pay" is all in the player's head, at least in the standard system.

How slot machines work

What are the odds?

In a modern slot machine, the odds of hitting a particular symbol or combination of symbols depends on how the virtual reel is set up. As we saw in the last section, each stop on the actual reel may correspond to more than one stop on the virtual reel. Simply put, the odds of hitting a particular image on the actual reel depend on how many virtual stops correspond to the actual stop.

In a typical weighted slot machine, the top jackpot stop (the one with the highest-paying jackpot image) for each reel corresponds to only one virtual stop. This means that the chance of hitting the jackpot image on one reel is 1 in 64. If all of the reels are set up the same way, the chances of hitting the jackpot image on all three reels is 1 in 64 3 , or 262,144. For machines with a bigger jackpot, the virtual reel may have many more stops. This decreases the odds of winning that jackpot considerably.

The losing blank stops above and below the jackpot image may correspond to more virtual stops than other images. Consequently, a player is most likely to hit the blank stops right next to the winning stop. This creates the impression that they "just missed" the jackpot, which encourages them to keep gambling, even though the proximity of the actual stops is inconsequential.

A machine's program is carefully designed and tested to achieve a certain payback percentage. The payback percentage is the percentage of the money that is put in that is eventually paid out to the player. With a payback percentage of 90, for example, the casino would take about 10 percent of all money put into the slot machine and give away the other 90 percent. With any payback percentage under a 100 (and they're all under 100), the casino wins over time.

In most gambling jurisdictions, the law requires that payback percentages be above a certain level (usually somewhere around 75 percent). The payback percentage in most casino machines is much higher than the minimum -- often in the 90- to 97-percent range. Casinos don't want their machines to be a lot tighter than their competitors' machines or the players will take their business elsewhere.

The odds for a particular slot machine are built into the program on the machine's computer chip. In most cases, the casino cannot change the odds on a machine without replacing this chip. Despite popular opinion, there is no way for the casino to instantly "tighten up" a machine.

Machines don't loosen up on their own either. That is, they aren't more likely to pay the longer you play. Since the computer always pulls up new random numbers, you have exactly the same chance of hitting the jackpot every single time you pull the handle. The idea that a machine can be "ready to pay" is all in the player's head, at least in the standard system.

When you hit the slot machines in a casino, you'll have dozens of gaming options. Machines come with varying numbers of reels, for example, and many have multiple pay lines.

Most machines with multiple pay lines let players choose how many lines to play. For the minimum bet, only the single line running straight across the reels counts. If the player puts more money in, he or she can play the additional horizontal lines above and below the main pay line or the diagonal lines running across the reels.

For machines with multiple bet options, whether they have multiple pay lines or not, players will usually be eligible for the maximum jackpot only when they make the maximum bet. For this reason, gambling experts suggest that players always bet the maximum.

There are several different payout schemes in modern slot machines. A standard flat top or straight slot machine has a set payout amount that never changes. The jackpot payout in a progressive machine, on the other hand, steadily increases as players put more money into it, until somebody wins it all and the jackpot is reset to a starting value. In one common progressive setup, multiple machines are linked together in one computer system. The money put into each machine contributes to the central jackpot. In some giant progressive games, machines are linked up from different casinos all across a city or even a state.

Some slot-machine variations are simply aesthetic. Video slots operate the same way as regular machines, but they have a video image rather than actual rotating reels. When these games first came out, players were very distrustful of them; without the spinning reels, it seemed like the games were rigged. Even though the reels and handles in modern machines are completely irrelevant to the outcome of the game, manufacturers usually include them just to give players the illusion of control.

These are only a few of today's popular slot variations. Game manufacturers continue to develop new sorts of machines with interesting twists on the classic game. A lot of these variations are built around particular themes. There are now slot games based on television shows, poker, craps and horse racing, just to name a few.

To learn more about modern slot machines, including strategies to increase your chances of winning, check out the links below.

Best slot machines by payout percentage

Sick of playing slot machines with rubbish payouts? Join the club!

To solve that exact problem we’ve put together a list of the best slots by payout percentage so you know that the machines your playing are the best they can possibly be.

Top 12 online slots by RTP

Click ‘play now’ buttons to visit an online casino offering the game:

Top 50 slots by payouts

Click name of slot machine to visit a casino offering the game:

Best payout slot machines by software provider

Whilst our comprehensive table of payout percentages for slot machines is undoubtedly illuminating, we have gone one step further in trying to help you find the best online slots.

This graph shows the eight main software providers for online slots and the average payout percentage across all of their games. Essentially it shows you which providers apply the smallest ‘house edge’ and thus produce the best slot machines for players.

RTP % by slot manufacturer

There are a couple of things that really stand out when you look closely at the graph:

• Amaya slots are by far and away the worst slot machines for payouts with a 92% RTP average (more on that later).


• Netent make the most player friendly slot games averaging a 96.51% payout percentage.


• The majority of companies are within 1% of each other setting an online industry standard of about 95% for slot payouts.


• Online slots have a comparatively impressive payout percentage across the board as compared to land-based slot machines (85% average), with upwards of 90% representing a kind of industry standard.

We’ve also built specific pages which breaks down the games offered by each brand:

Why are amaya payouts so bad?

Amaya lags quite significantly behind the others with a payout percentage of 92%… why are they so far behind the rest?

Amaya are a canadian company based in montreal and after their purchase of the parent company of pokerstars and full tilt poker in 2014, became the world’s largest public listed online gambling games company.

It may be therefore, that as market leaders there is less pressure on amaya to match or better their competitors’ payout percentages. Amaya have also recently purchased several other slots providers including aristrocrat and chartwell. Both companies were known for their low return to player percentages and therefore could be dragging the amaya averages down.

However at the core of this issue is the fact that amaya are a major player in the creation of software for real world slot machines and as such clearly want to bring the lower land based percentages to the online scene (how very noble of them indeed).

Slot machine payouts vs other casino games

Plenty of useful conclusions can be drawn from simply looking at the payout percentages of different slots games and software providers.

However… it is also important to look at the RTP percentages of slots as compared to other online casino games.

RTP percentages: slots vs other casino games

*graph assumes a player is playing the most favourable variation of the game and is employing perfect strategy.

Keno is the obvious place to start when looking at this data, as its RTP percentage is significantly lower than any other at 73% (avoid at all costs folks). Blackjack has a much higher average RTP percentage of 99.50% and when played correctly is the most player friendly casino game there is.

It’s pretty difficult to land a significant payday playing blackjack. You’ve got to get on a seriously hot streak which lasts a significant amount of time to make a lot of money. Slots machines, although with an average RPT of 95.67%, do offer the chance to score that big payout and it could be argued that sacrificing a bit of house edge to get that opportunity is worth it.

As a side note blackjack’s very low house edge is why it’s pretty much always excluded from wagering requirements for online casino bonuses. With the bonus money added to expected returns when clearing the bonus it can actually produce an edge for the player if perfect strategy is employed.

How do RTP percentages work?

RTP or payout percentages are a representation of the average rate at which a game – be it slots or otherwise – pays out to players, as compared to the total amount that players stake. In general, online slots games have a payout percentage of around 95% and in the simplest possible terms this means that on average the game will pay out £95 for every £100 staked on it.

That does not mean that every player is guaranteed £95 worth of payout if and when they stake £100 however, as the percentages are based upon a very high number of spins. General probability and more simply the law of averages, means that an individual player could still win far more than they stake or lose considerably more than 5% in one session or over an extended period of time.

What it does mean is that on average the online casino or game provider will take 5% of the money staked on the game for themselves, and that is called the ‘house edge’.

How are slot machine payouts calculated?

For players… RTP = (total amount returned to players) / (total amount bet by players). That calculation will always return the result in the form of a decimal (e.G. 0.95) and it can then simply be translated into a percentage, which in that example would be 95%.

For the casinos… the number of symbols built into the game, the amount of combinations of those symbols which provide a payout, the value of those payouts and the probability of those combinations occurring combine to produce the games overall RTP %.

Why do slots have different payouts?

Online slot games software providers have no real restrictions placed upon them in terms of the initial RTP percentage they build into their games. The UK gambling commission nor any other regulatory body of note impose a statutory minimum upon online slots games and as such the providers can set the level themselves.

Levels are determined by the paytable and symbols in the game, these differ from game to game and therefore payouts differ as well. They are set to make machines attractive to players whilst still providing a house edge for the casino. The best slots from a players point of view are usually always those with the highest possible payout percentages.

Do online slots or land based have better payouts?

The best slot machine games, where payouts are concerned, are always online based. The percentage falls dramatically live as compared with online.

Where the general online average RTP percentage tends to hover around 95%, land based casinos can – and often do – offer percentages as low as 75%. That figure in fact, is one which is often linked to machines in las vegas where the state imposed minimum is indeed only 75%.

Other global regulatory bodies however, do impose a more stringent minimum on physical slot machines, with the state of new jersey requiring 83% and the state of mississippi 80% for example.

In the UK meanwhile, the UK gambling commission does not actually impose any statutory minimum. It does dictate however, that all machines must display their RTP percentages clearly to players and that does tend to prevent casinos and bookmakers from allowing the percentages to fall too low as to make games unfair.

Can casinos change payout percentages?

The answer to this question tends to be no, but the explanation of that answer differs in terms of live and online slots games.

Online casinos

To deal with online games first, as we have mentioned online there is no statutory minimum RTP percentage which allows providers to set their own levels. What they cannot do however, is to routinely alter or skew those percentages or to lie about them to their customers.

This is prevented by the necessity of online slots providers to have their games regularly tested by independent testing boards. These boards must themselves by licensed by the relevant legislative bodies and will check that a provider’s games generate random combinations, are not biased towards or away from certain combinations and deliver the RTP percentage that they claim. If you stick to online gaming sites which are legit and registered with testing boards such as ecogra in the UK, itech labs in australia or gaming laboratories international in the USA therefore, you can be sure that the games have fair and consistent RTP percentages.

Live casinos

With physical slot machines, the payout percentage tends to be set when the imbedded software is originally written and as such can only be altered by the physical switching of the software or firmware.

That is a time consuming and difficult process, and is one that is also often subject to different rules according to the jurisdiction in which the machine is operated. In the US state of new jersey for example, each machine is fitted with a tamper proof seal to ensure that any switch of software can only be carried out in the presence of a gaming control board official. All of that, together with the fact that it is an almost universally applied rule that the RTP percentage for a machine must be clearly displayed to players, makes it very difficult therefore for casinos and other slots providers to change percentages whenever they want.

But essentially in a live environment it can be done, it’s just quite difficult to do it.

How to find the payout percentage on a slot machine

Some people might want to know how to find the payout percentage on a slot machine. Sadly, it’s not something that’s printed on most games — at least not here in the united states.

Understanding this topic involves some rudimentary understanding of probability as it relates to casino gambling. You’ll need to understand three separate concepts thoroughly:

1. Payback percentage


2. House edge


3. Return to player

This post explains each of those in enough detail that even a beginner should understand what they mean.

Some basic facts related to probability, the house edge, payback percentage, and return to player

Probability is the branch of mathematics that deals with how likely an event is to happen. If you want to measure how likely you are to win a jackpot on a slot machine, probability is the way to figure that out.

But the word also refers directly to that likelihood.

In other words, if I say the probability of getting heads when I flip a coin is 50%, I’m not talking about that branch of mathematics. I’m talking about the actual statistical likelihood of that event.

You should understand a few things about probability in general.

Probability is always a number between 0 and 1. An event with a probability of 0 will never happen, and an event with a probability of 1 will always happen. The closer to 1 the probability is, the more likely the event is to happen.

Probability can be expressed multiple ways. It can be expressed as a fraction, a decimal, a percentage, or as odds. The probability of getting heads on a coin flip can be expressed as 1/2, 0.5, 50%, or 1 to 1.

An event’s probability is the number of ways it can happen divided by the total number of possible outcomes. When you’re discussing a coin toss, you have two possible outcomes. Only one of those is heads. That makes the probability 1/2.

The probability that an event will occur added to the probability that an event won’t occur always equals 1. Therefore, if you know the probability that something will happen, you also automatically know the probability that it won’t happen, and vice versa.

The house edge is a statistical measure of how much the house expects to win (on average, over the long run) from every bet you make on a game. The house edge is a theoretical number that accounts for the probability of winning versus the probability of losing AND the payout if you win.

All casino games carry a house edge. In the short run, it doesn’t matter much, but in the long run, it’s the most important thing.

If I say a game has a house edge of 4%, this means that over time, you should average a loss of $4 for every $100 you bet on the game. This is a long run statistical average, though. In the short run, you’re unlikely to see results that mirror the house edge.

The return to player and the payback percentage are the same thing. Some writers use one to refer to the statistical expectation and the other to refer to the actual results, but most writers use these terms interchangeably.

The payback percentage added to the house edge always equals 100%. The payback percentage is the amount of each bet that you get back, and the house edge is the amount of each bet that the casino wins. Again, these numbers are on average over the long run.

A game with a 4% house edge has a 96% payback percentage.

In the united states, slot machine payback percentages are impossible to calculate and not posted on gambling machines. To calculate the house edge or the payback percentage for a casino game, you need two pieces of data:

1. The probability of winning


2. The amount of money you’ll win (the payoff)

Slot machines include their payouts on their pay tables, but they don’t include the probability of achieving any of the winning outcomes.

In some countries, the payback percentage is posted on the machines, but not in the united states.

To make things even worse for a slot machine player, the random number generator program can be set differently even if the slot machine is identical to the one next to it. You could be playing the big lebowski slots at choctaw casino in durant, oklahoma, and your buddy could be playing the identical machine right next to you.

The payback percentage on his machine might be 94%, and the payback percentage on your machine might only be 88%.

The difference comes from how the probabilities are weighted for each symbol. On one game, the bars might show up 1/4 of the time, but on the next, they might only come up 1/8 of the time.

This has an obvious effect on the payback percentage.

The payback percentage would be easy to calculate if you knew the probabilities. The payback percentage is just the total expected value of all the possible outcomes on the machine.

Let’s assume you have 1000 possible reel combinations. Let’s also assume that if you got each of those in order, from 1 to 1000, you’d win 900 coins.

The payback percentage for that game would be 90%.

You’d put 1000 coins in, and you’d have 900 coins left after a statistically perfect sampling of 1000 spins.

If you knew the payback percentage and house edge for a slot machine game, you could predict your theoretical cost of playing that game per hour in the long run. You’d only need to multiply the numbers of bets you made per hour by the size of those bets. Then you’d multiply that by the house edge to get your predicted loss.

Most slots players make 600 spins per hour. Let’s assume you’re playing on a dollar machine and betting three coins on every spin, or $3 per spin. You’re putting $1,800 per hour into action.

If the slot machine had a 90% payback percentage, you’d lose $180 per hour on that machine. You’d have $1,800 at the start of the hour and $1,620 at the end of the hour — assuming you saw statistically predicted results.

In the real world, though, where you’d be seeing short-term results, you’d see some hours where you won and some hours where you lost. If you played long enough, the law of large numbers would ensure that you’d eventually see the statistically predicted results.

But in the long run, the math will ensure that the casino will win a net profit.

How you could calculate a payback percentage based on actual results

Of course, you have some data that you can directly observe when you’re playing slot machines.

But tracking this data and calculating the payback percentage on a specific session can add to your enjoyment of any slot machine game. It can make you more mindful because you’ll be paying more attention to what’s happening.

Start by tracking how many spins you’re making per hour. This is easy to do, but it takes more effort than you might think. It might help to get one of those clicky things people use to count stuff with. You will probably also need a stopwatch of some kind. I just use the timer function on my phone.

Make a note (mental is fine) of how much you’re betting per spin. It helps to bet the same amount.

Also note how much money you started with so that you can calculate how much you’ve won or lost. The slot machine will convert your money into credits. The easiest thing to do is to keep up with how many credits you had at the beginning of the session and again at the end of the session.

Now, let’s do the math using a hypothetical 45-minute session.

I made 300 spins in 45 minutes. I was betting $3 per spin, and I started with $600.

After my playing session, I had $500 left. At times I was up, and at times I was down.

But my net loss was $100. (my starting bankroll was $600, and I finished with $500.)

Over 300 spins, that means I lost an average per spin of 33 cents. $100 in losses divided by 300 spins is 33.33 cents per spin.

How much was I betting per spin?

Since I was playing a $1 machine, and my max bet was three coins, I was risking $3 per spin.

33 cents is 11% of $3, which means my actual loss was 11%. The machine paid back 89% for the session.

Does this mean that the payback percentage for the machine is 89%?

In the scheme of things, 450 spins is a small sample size. To have any confidence in your statistics, you really need to have at least 5,000 spins under your belt.

Even then, depending on how volatile the game is, your actual results might be wildly different from the mathematically expected payback percentage.

Here’s another example that will prove that point.

My friend leo went to the winstar last weekend and played the $5 slots. He started with $3,000, and when he left, he had $4,800, which means he had an $1,800 profit for the day.

He played for seven hours.

I’ve watched leo play. He’s slow, but not much slower than average. He makes about 500 spins per hour.

This means that he made about 3,500 spins.

$1,800 in winnings divided by 3,500 spins is an average win of 51 cents per spin.

Since he was betting $5 per spin, his return was 10.3%.

His actual return for the trip on that slot machine was 110.3%.

I have friends who design slot machines for a living — more than one, in fact. They’ll be happy to tell anyone who asks that the algorithm is never set up to have a payback percentage of more than 100%.

What about the casinos that advertise a specific payback percentage?

Some casinos advertise a specific payback percentage. This is almost always stated as an “up to” number.

So you might see an ad for a casino that says, “payback percentages up to 98%!”

They’re almost certainly telling the truth, too. They probably have one slot machine in their casino that has a payback percentage of 98%. Of course, it isn’t labeled, so you don’t know which one it is.

And in the short run, which is what you’re going to be playing in as an individual gambler, there’s not much difference between a 98% payback percentage and a 92% payback percentage. You could walk away a winner or a loser at either setting.

Also, keep in mind that the games aren’t designed to tighten up after a win and loosen up after a lot of losing spins. That’s not how it works at all.

The machines are designed to allow you to win a certain specific percentage of the time because of the probability. Then there’s an average amount that you’ll win based on the payout for the specific combination of symbols that you hit.

But every spin of the reels on a slot machine is an independent event. You can hit a jackpot on a spin, and your probability of hitting the jackpot on the next spin hasn’t changed at all.

What about the denominations and location reports I see advertised on the internet?

You’ll find websites like strictly slots and american casino guide which post payback percentages for specific denominations and specific casinos. These are AVERAGES.

These averages have little bearing on the machine that you’re sitting in front of.

For example,
you might be looking at a casino that reports an average payback percentage of 94% on its dollar slot machines. That casino might have half their machines paying off at 90% and the other half paying off at 98%.

And you won’t be able to differentiate between the two because the hit ratio might be the same from one of those machines to another.

What do hit ratio and volatility have to do with it?

The hit ratio is the percentage of time that you can expect to hit a winning combination on a slot machine. Something like 30% isn’t unusual, but it can vary 10% or more in either direction. The casinos want you to a hit a winning combination often enough that you won’t lose interest in playing the game.

But hit ratio is only part of the equation. The average size of the prize amounts is also important. Volatility takes this into account. A game that hits less often but has higher average prize amounts might have the same payback percentage as a game that hits more often but with lower payouts.

Either way, in the short run, it will be all but impossible to discover this number, too.

If you wanted to, you could track how many spins resulted in wins for you and calculate the percentage, but you’re facing the same obstacle you are with the overall payback percentage of the machine.

You just don’t know what it’s programmed to accomplish in the long run.

Online slot machines

Some online casinos post the payback percentages for their slot machine games. I think this information is of limited use, but I also think it’s fairer to the gambler than not providing them with that information.

After all, table games are transparent. You can calculate the house edge for any casino table game there is because they all use random number generators with known quantities — cards, dice, and wheels.

There’s been a push to label food, both at the grocery store and at restaurants, with nutritional information that includes caloric amounts.

Requiring casinos to provide similar information about their gambling machines only makes sense.

We’ll see if it ever happens, though.

Conclusion

You can’t find the payout percentage on a slot machine — at least not in the united states.
I’ve heard that you can get this information on slot machines in europe, but I’ve never seen an actual photograph of this kind of labeling.
You can, though, have some fun calculating actual payback percentages in the short run. This at least gives you something to keep track of while you’re playing slots, which is honestly one of the more mindless activities in the casino.

Michael stevens has been researching and writing topics involving the gambling industry for well over a decade now and is considered an expert on all things casino and sports betting. Michael has been writing for gamblingsites.Org since early 2016. .

Michael stevens has been researching and writing topics involving the gambling industry fo .

Slot machine payback percentages

The house edge at slot machines isn't based on how lucky the players are, it is based on the pre-programmed electronic software used. And, that house edge varies from casino to casino and from geographic location and state to state.

Don't be fooled by a billboard that says "our slots pay 99%" because that only pertains to a small number of machines, not the casino's overall house edge. All video slot machines (including poker) use a random number generator to provide accurate odds for the player and the house.

The number of winning hands (symbols) in any program is mathematically proven before the slots hit the gaming floor, and while the odds vary for each player (because this really is gambling), overall, the anticipated house edge will eventually be achieved.

The house edge at slots

Each gaming jurisdiction requires all slot machines to be registered and all slot manufacturers must submit their programming and math charts to the state gaming office, such as the nevada gaming control board. While the state may only require a minimum payback of 86-percent, most video poker and slot machines pay more. The average payback in nevada is lowest on penny slots at about 90-percent. Dollar slots and some deuces-wild poker machines have the highest payback at nearly 99-percent.

Of course just because a machine has a payback of 99 percent does not mean you will win back $99 for every $100 you play through the machine. That payback amount is an average. Over the course of an evening of gambling, you might lose $500 or win $5,000. That's the beauty of the gamble, right? And, the casino doesn't care either way, because they win an average of whatever their house edge is over the course of the month.

How does that 99-percent work for you? Aside from the ups and downs of jackpots and dry spells, your entertainment dollar is going to be based on how long you play. If you play a machine that takes $3 per spin and you pull the handle 10-times an hour, you are playing $3 x 10 x 60 = $1,800 in action. At 99-percent house edge, your play costs $18 an hour. Some nights you'll go home ready to kick the wall, and other nights you be singing a happy tune because you hit a jackpot and skated out with hundreds. That's gambling.

Play within your means

As a general rule, the higher denomination slot machines have a greater overall payback percentage that the lower ones. That's great for those with a healthy bankroll, but you'll need to play the games that offer you the best bang for the buck. The worst thing a player can do is to play any game for more money than they can afford to lose or at a higher denomination than their bankroll will handle.

Another consideration is making sure you can qualify for any bonus screen or royal flush payoff. If you want to wile away the hours playing a single nickel in a machine, that's great. Enjoy. You won't win or lose much and you'll probably go home happier than most players. But your play comes with a catch!

That catch is that the house edge provided for each machine includes the big jackpots (such as a royal flush), and if you play below the minimum to reach the bonus screen, the house edge is much higher! You won't lose much, but you'll never win more than a couple of dollars.

The best option

The best option is to play the games you enjoy most, and make sure you read the help screen so you know how many credits it takes to qualify for at least the lowest progressive jackpot and the bonus screen (or royal flush at video poker). As a recreational player, your first goal is to have fun. If you only visit the casino occasionally the overall payback of the machine won't make much of a difference. If you visit regularly, make sure you join the player's club and play within your means!

Casino slot machine winning percentage

This guide, written by casino math professor robert hannum, contains a brief, non-technical discussion of the basic mathematics governing casino games and shows how casinos make money from these games. The article addresses a variety of topics, including house advantage, confusion about win rates, game volatility, player value and comp policies, casino pricing mistakes, and regulatory issues. Statistical advantages associated with the major games are also provided.

Slot machine	software	RTP%
monopoly big event	barcrest
Understanding casino math
Introduction Why is mathematics important? The house edge Probability versus odds Confusion about win rate Volatility and risk Player value and complimentaries Gaming regulation and mathematics Summary tables for house advantage At its core the business of casino gaming is pretty simple. Casinos make money on their games because of the mathematics behind the games. As nico zographos, dealer-extraordinaire for the 'greek syndicate' in deauville, cannes, and monte carlo in the 1920s observed about casino gaming: "there is no such thing as luck. It is all mathematics." With a few notable exceptions, the house always wins - in the long run - because of the mathematical advantage the casino enjoys over the player. That is what mario puzo was referring to in his famous novel fools die when his fictional casino boss character, gronevelt, commented: "percentages never lie. We built all these hotels on percentages. We stay rich on the percentage. You can lose faith in everything, religion and god, women and love, good and evil, war and peace. You name it. But the percentage will always stand fast." Puzo is, of course, right on the money about casino gaming. Without the "edge," casinos would not exist. With this edge, and because of a famous mathematical result called the law of large numbers, a casino is guaranteed to win in the long run. Why is mathematics important? Critics of the gaming industry have long accused it of creating the name "gaming" and using this as more politically correct than calling itself the "gambling industry." the term "gaming," however, has been around for centuries and more accurately describes the operators' view of the industry because most often casino operators are not gambling. Instead, they rely on mathematical principles to assure that their establishment generates positive gross gaming revenues. The operator, however, must assure the gaming revenues are sufficient to cover deductions like bad debts, expenses, employees, taxes and interest. Despite the obvious, many casino professionals limit their advancements by failing to understand the basic mathematics of the games and their relationships to casino profitability. One casino owner would often test his pit bosses by asking how a casino could make money on blackjack if the outcome is determined simply by whether the player or the dealer came closest to 21. The answer, typically, was because the casino maintained "a house advantage." this was fair enough, but many could not identify the amount of that advantage or what aspect of the game created the advantage. Given that products offered by casinos are games, managers must understand why the games provide the expected revenues. In the gaming industry, nothing plays a more important role than mathematics. Mathematics should also overcome the dangers of superstitions. An owner of a major las vegas strip casino once experienced a streak of losing substantial amounts of money to a few "high rollers." he did not attribute this losing streak to normal volatility in the games, but to bad luck. His solution was simple. He spent the evening spreading salt throughout the casino to ward off the bad spirits. Before attributing this example to the idiosyncrasies of one owner, his are atypical only in their extreme. Superstition has long been a part of gambling - from both sides of the table. Superstitions can lead to irrational decisions that may hurt casino profits. For example, believing that a particular dealer is unlucky against a particular (winning) player may lead to a decision to change dealers. As many, if not most, players are superstitious. At best, he may resent that the casino is trying to change his luck. At worst, the player may feel the new dealer is skilled in methods to "cool" the game. Perhaps he is even familiar with stories of old where casinos employed dealers to cheat "lucky" players. Understanding the mathematics of a game also is important for the casino operator to ensure that the reasonable expectations of the players are met. For most persons, gambling is entertainment. It provides an outlet for adult play. As such, persons have the opportunity for a pleasant diversion from ordinary life and from societal and personal pressures. As an entertainment alternative, however, players may consider the value of the gambling experience. For example, some people may have the option of either spending a hundred dollars during an evening by going to a professional basketball game or at a licensed casino. If the house advantage is too strong and the person loses his money too quickly, he may not value that casino entertainment experience. On the other hand, if a casino can entertain him for an evening, and he enjoys a "complimentary" meal or drinks, he may want to repeat the experience, even over a professional basketball game. Likewise, new casino games themselves may succeed or fail based on player expectations. In recent years, casinos have debuted a variety of new games that attempt to garner player interest and keep their attention. Regardless of whether a game is fun or interesting to play, most often a player will not want to play games where his money is lost too quickly or where he has a exceptionally remote chance of returning home with winnings. Mathematics also plays an important part in meeting players' expectations as to the possible consequences of his gambling activities. If gambling involves rational decision-making, it would appear irrational to wager money where your opponent has a better chance of winning than you do. Adam smith suggested that all gambling, where the operator has an advantage, is irrational. He wrote "there is not, however, a more certain proposition in mathematics than that the more tickets [in a lottery] you advertise upon, the more likely you are a loser. Adventure upon all the tickets in the lottery, and you lose for certain; and the greater the number of your tickets, the nearer you approach to this certainty." Even where the house has an advantage, however, a gambler may be justified if the amount lost means little to him, but the potential gain would elevate him to a higher standing of living. For example, a person with an annual income of $30,000 may have $5 in disposable weekly income. He could save or gamble this money. By saving it, at the end of a year, he would have $260. Even if he did this for years, the savings would not elevate his economic status to another level. As an alternative, he could use the $5 to gamble for the chance to win $1 million. While the odds of winning are remote, it may provide the only opportunity to move to a higher economic class. Since the casino industry is heavily regulated and some of the standards set forth by regulatory bodies involve mathematically related issues, casino managers also should understand the mathematical aspects relating to gaming regulation. Gaming regulation is principally dedicated to assuring that the games offered in the casino are fair, honest, and that players get paid if they win. Fairness is often expressed in the regulations as either requiring a minimum payback to the player or, in more extreme cases, as dictating the actual rules of the games offered. Casino executives should understand the impact that rules changes have on the payback to players to assure they meet regulatory standards. Equally important, casino executives should understand how government mandated rules would impact their gaming revenues. The player's chances of winning in a casino game and the rate at which he wins or loses money depends on the game, the rules in effect for that game, and for some games his level of skill. The amount of money the player can expect to win or lose in the long run - if the bet is made over and over again - is called the player's wager expected value (EV), or expectation. When the player's wager expectation is negative, he will lose money in the long run. For a $5 bet on the color red in roulette, for example, the expectation is -$0.263. On the average the player will lose just over a quarter for each $5 bet on red. When the wager expectation is viewed from the casino's perspective (i.E., the negative of the player's expectation) and expressed as a percentage, you have the house advantage. For the roulette example, the house advantage is 5.26% ($0.263 divided by $5). The formal calculation is as follows: EV = (+5)(18/38) + (-5)(20/38) = -0.263 (house advantage = 0.263/5 = 5.26%) When this EV calculation is performed for a 1-unit amount, the negative of the resulting value is the house edge. Here are the calculations for bets on a single-number in double-zero and single-zero roulette. Double-zero roulette (single number bet): EV = (+35)(1/38) + (-1)(37/38) = -0.053 (house advantage = 5.3%) Single-zero roulette (single number bet): EV = (+35)(1/37) + (-1)(36/37) = -0.027 (house advantage = 2.7%) The house advantage represents the long run percentage of the wagered money that will be retained by the casino. It is also called the house edge, the "odds" (i.E., avoid games with bad odds), or just the "percentage" (as in mario puzo's fools die). Although the house edge can be computed easily for some games - for example, roulette and craps - for others it requires more sophisticated mathematical analysis and/or computer simulations. Regardless of the method used to compute it, the house advantage represents the price to the player of playing the game. Because this positive house edge exists for virtually all bets in a casino (ignoring the poker room and sports book where a few professionals can make a living), gamblers are faced with an uphill and, in the long run, losing battle. There are some exceptions. The odds bet in craps has zero house edge (although this bet cannot be made without making another negative expectation wager) and there are a few video poker machines that return greater than 100% if played with perfect strategy. Occasionally the casino will even offer a promotion that gives the astute player a positive expectation. These promotions are usually mistakes - sometimes casinos don't check the math - and are terminated once the casino realizes the player has the edge. But by and large the player will lose money in the long run, and the house edge is a measure of how fast the money will be lost. A player betting in a game with a 4% house advantage will tend to lose his money twice as fast as a player making bets with a 2% house edge. The trick to intelligent casino gambling - at least from the mathematical expectation point of view - is to avoid the games and bets with the large house advantages. Some casino games are pure chance - no amount of skill or strategy can alter the odds. These games include roulette, craps, baccarat, keno, the big-six wheel of fortune, and slot machines. Of these, baccarat and craps offer the best odds, with house advantages of 1.2% and less than 1% (assuming only pass/come with full odds), respectively. Roulette and slots cost the player more - house advantages of 5.3% for double-zero roulette and 5% to 10% for slots - while the wheel of fortune feeds the casino near 20% of the wagers, and keno is a veritable casino cash cow with average house advantage close to 30%. Games where an element of skill can affect the house advantage include blackjack, video poker, and the four popular poker-based table games: caribbean stud poker, let it ride, three card poker, and pai gow poker. For the poker games, optimal strategy results in a house edge in the 3% to 5% range (CSP has the largest house edge, PGP the lowest, with LIR and TCP in between). For video poker the statistical advantage varies depending on the particular machine, but generally this game can be very player friendly - house edge less than 3% is not uncommon and some are less than 1% - if played with expert strategy. Blackjack, the most popular of all table games, offers the skilled player some of the best odds in the casino. The house advantage varies slightly depending on the rules and number of decks, but a player using basic strategy faces little or no disadvantage in a single-deck game and only a 0.5% house edge in the common six-deck game. Despite these numbers, the average player ends up giving the casino a 2% edge due to mistakes and deviations from basic strategy. Complete basic strategy tables can be found in many books and many casino-hotel gift shops sell color-coded credit card size versions. Rule variations favorable to the player include fewer decks, dealer stands on soft seventeen (worth 0.2%), doubling after splitting (0.14%), late surrender (worth 0.06%), and early surrender (uncommon, but worth 0.24%). If the dealer hits soft seventeen it will cost you, as will any restrictions on when you can double down. Probability represents the long run ratio of (# of times an outcome occurs) to (# of times experiment is conducted). Odds represent the long run ratio of (# of times an outcome does not occur) to (# of times an outcome occurs). If a card is randomly selected from a standard deck of 52 playing cards, the probability it is a spade is 1/4; the odds (against spade) are 3 to 1. The true odds of an event represent the payoff that would make the bet on that event fair. For example, a bet on a single number in double-zero roulette has probability of 1/38, so to break even in the long run a player would have to be paid 37 to 1 (the actual payoff is 35 to 1). There are all kinds of percentages in the world of gaming. Win percentage, theoretical win percentage, hold percentage, and house advantage come to mind. Sometimes casino bosses use these percentages interchangeably, as if they are just different names for the same thing. Admittedly, in some cases this is correct. House advantage is just another name for theoretical win percentage, and for slot machines, hold percentage is (in principle) equivalent to win percentage. But there are fundamental differences among these win rate measurements. The house advantage - the all-important percentage that explains how casinos make money - is also called the house edge, the theoretical win percentage, and expected win percentage. In double-zero roulette, this figure is 5.3%. In the long run the house will retain 5.3% of the money wagered. In the short term, of course, the actual win percentage will differ from the theoretical win percentage (the magnitude of this deviation can be predicted from statistical theory). The actual win percentage is just the (actual) win divided by the handle. Because of the law of large numbers - or as some prefer to call it, the law of averages - as the number of trials gets larger, the actual win percentage should get closer to the theoretical win percentage. Because handle can be difficult to measure for table games, performance is often measured by hold percentage (and sometimes erroneously called win percentage). Hold percentage is equal to win divided by drop. In nevada, this figure is about 24% for roulette. The drop and hold percentage are affected by many factors; we won't delve into these nor the associated management issues. Suffice it to say that the casino will not in the long term keep 24% of the money bet on the spins of roulette wheel - well, an honest casino won't. To summarize: house advantage and theoretical win percentage are the same thing, hold percentage is win over drop, win percentage is win over handle, win percentage approaches the house advantage as the number of plays increases, and hold percentage is equivalent to win percentage for slots but not table games. · hold % = win/drop · win % (actual) = win/handle · H.A. = theoretical win % = limit(actual win %) = limit(win/handle) · hold percentage ¹ house edge Furthermore, the house advantage is itself subject to varying interpretations. In let it ride, for example, the casino advantage is either 3.51% or 2.86% depending on whether you express the advantage with respect to the base bet or the average bet. Those familiar with the game know that the player begins with three equal base bets, but may withdraw one or two of these initial units. The final amount put at risk, then, can be one (84.6% of the time assuming proper strategy), two (8.5%), or three units (6.9%), making the average bet size 1.224 units. In the long run, the casino will win 3.51% of the hands, which equates to 2.86% of the money wagered. So what's the house edge for let it ride? Some prefer to say 3.51% per hand, others 2.86% per unit wagered. No matter. Either way, the bottom line is the same either way: assuming three $1 base bets, the casino can expect to earn 3.5¢ per hand (note that 1.224 x 0.0286 = 0.035). The question of whether to use the base bet or average bet size also arises in caribbean stud poker (5.22% vs. 2.56%), three card poker (3.37% vs. 2.01%), casino war (2.88% vs. 2.68%), and red dog (2.80% vs. 2.37%). For still other games, the house edge can be stated including or excluding ties. The prime examples here are the player (1.24% vs. 1.37%) and banker (1.06% vs. 1.17%) bets in baccarat, and the don't pass bet (1.36% vs. 1.40%) in craps. Again, these are different views on the casino edge, but the expected revenue will not change. That the house advantage can appear in different disguises might be unsettling. When properly computed and interpreted, however, regardless of which representation is chosen, the same truth (read: money) emerges: expected win is the same. Statistical theory can be used to predict the magnitude of the difference between the actual win percentage and the theoretical win percentage for a given number of wagers. When observing the actual win percentage a player (or casino) may experience, how much variation from theoretical win can be expected? What is a normal fluctuation? The basis for the analysis of such volatility questions is a statistical measure called the standard deviation (essentially the average deviation of all possible outcomes from the expected). Together with the central limit theorem (a form of the law of large numbers), the standard deviation (SD) can be used to determine confidence limits with the following volatility guidelines: Volatility analysis guidelines · only 5% of the time will outcomes will be more than 2 SD's from expected outcome · almost never (0.3%) will outcomes be more than 3 SD's from expected outcome Obviously a key to using these guidelines is the value of the SD. Computing the SD value is beyond the scope of this article, but to get an idea behind confidence limits, consider a series of 1,000 pass line wagers in craps. Since each wager has a 1.4% house advantage, on average the player will be behind by 14 units. It can be shown (calculations omitted) that the wager standard deviation is for a single pass line bet is 1.0, and for 1,000 wagers the SD is 31.6. Applying the volatility guidelines, we can say that there is a 95% chance the player's actual win will be between 49 units ahead and 77 units behind, and almost certainly between 81 units ahead and 109 units behind. A similar analysis for 1,000 single-number wagers on double-zero roulette (on average the player will be behind 53 units, wager SD = 5.8, 1,000 wager SD = 182.2) will yield 95% confidence limits on the player win of 311 units ahead and 417 units behind, with win almost certainly between 494 units ahead and 600 units behind. Note that if the volatility analysis is done in terms of the percentage win (rather than the number of units or amount won), the confidence limits will converge to the house advantage as the number of wagers increases. This is the result of the law of large numbers - as the number of trials gets larger, the actual win percentage should get closer to the theoretical win percentage. Risk in the gaming business depends on the house advantage, standard deviation, bet size, and length of play. Player value and complimentaries Using the house advantage, bet size, duration of play, and pace of the game, a casino can determine how much it expects to win from a certain player. This player earning potential (also called player value, player worth, or theoretical win) can be calculated by the formula: Earning potential = average bet ´ hours played ´ decisions per hour ´ house advantage For example, suppose a baccarat player bets $500 per hand for 12 hours at 60 hands per hour. Using a house advantage of 1.2%, this player's worth to the casino is $4,320 (500 ´ 12 ´ 60 ´ .012). A player who bets $500 per spin for 12 hours in double-zero roulette at 60 spins per hour would be worth about $19,000 (500 ´ 12 ´ 60 ´ .053). Many casinos set comp (complimentary) policies by giving the player back a set percentage of their earning potential. Although comp and rebate policies based on theoretical loss are the most popular, rebates on actual losses and dead chip programs are also used in some casinos. Some programs involve a mix of systems. The mathematics associated with these programs will not be addressed in this article. In an effort to entice players and increase business, casinos occasionally offer novel wagers, side bets, increased payoffs, or rule variations. These promotions have the effect of lowering the house advantage and the effective price of the game for the player. This is sound reasoning from a marketing standpoint, but can be disastrous for the casino if care is not taken to ensure the math behind the promotion is sound. One casino offered a baccarat commission on winning banker bets of only 2% instead of the usual 5%, resulting in a 0.32% player advantage. This is easy to see (using the well-known probabilities of winning and losing the banker bet): EV = (+0.98)(.4462) + (-1)(.4586) = 0.0032 (house advantage = -0.32%) A casino in biloxi, mississippi gave players a 12.5% edge on sic bo bets of 4 and 17 when they offered 80 to 1 payoffs instead of the usual 60 to 1. Again, this is an easy calculation. Using the fact that the probability of rolling a total of 4 (same calculation applies for a total of 17) with three dice is 1/72 (1/6 x 1/6 x 1/6 x 3), here are the expected values for both the usual and the promotional payoffs: Usual 60 to 1 payoff: EV = (+60)(1/72) + (-1)(71/72) = -0.153 (house advantage = 15.3%) Promotional 80 to 1 payoff: EV = (+80)(1/72) + (-1)(71/72) = +0.125 (house advantage = -12.5%) In other promotional gaffes, an illinois riverboat casino lost a reported $200,000 in one day with their "2 to 1 tuesdays" that paid players 2 to 1 (the usual payoff is 3 to 2) on blackjack naturals, a scheme that gave players a 2% advantage. Not to be outdone, an indian casino in california paid 3 to 1 on naturals during their "happy hour," offered three times a day, two days a week for over two weeks. This promotion gave the player a whopping 6% edge. A small las vegas casino offered a blackjack rule variation called the "free ride" in which players were given a free right-to-surrender token every time they received a natural. Proper use of the token led to a player edge of 1.3%, and the casino lost an estimated $17,000 in eight hours. Another major las vegas casino offered a "50/50 split" blackjack side bet that allowed the player to stand on an initial holding of 12-16, and begin a new hand for equal stakes against the same dealer up card. Although the game marketers claimed the variation was to the advantage of the casino, it turned out that players who exercised the 50/50 split only against dealer 2-6 had a 2% advantage. According to one pit boss, the casino suffered a $230,000 loss in three and a half days. In the gaming business, it's all about "bad math" or "good math." honest games based on good math with positive house advantage minimize the short-term risk and ensure the casino will make money in the long run. Players will get "lucky" in the short term, but that is all part of the grand design. Fluctuations in both directions will occur. We call these fluctuations good luck or bad luck depending on the direction of the fluctuation. There is no such thing as luck. It is all mathematics. Gaming regulation and mathematics Casino gaming is one of the most regulated industries in the world. Most gaming regulatory systems share common objectives: keep the games fair and honest and assure that players are paid if they win. Fairness and honesty are different concepts. A casino can be honest but not fair. Honesty refers to whether the casino offers games whose chance elements are random. Fairness refers to the game advantage - how much of each dollar wagered should the casino be able to keep? A slot machine that holds, on average, 90% of every dollar bet is certainly not fair, but could very well be honest (if the outcomes of each play are not predetermined in the casino's favor). Two major regulatory issues relating to fairness and honesty - ensuring random outcomes and controlling the house advantage - are inextricably tied to mathematics and most regulatory bodies require some type of mathematical analysis to demonstrate game advantage and/or confirm that games outcomes are random. Such evidence can range from straightforward probability analyses to computer simulations and complex statistical studies. Requirements vary across jurisdictions, but it is not uncommon to see technical language in gaming regulations concerning specific statistical tests that must be performed, confidence limits that must be met, and other mathematical specifications and standards relating to game outcomes. Summary tables for house advantage The two tables below show the house advantages for many of the popular casino games. The first table is a summary of the popular games and the second gives a more detailed breakdown. House advantages for popular casino games game house advantage roulette (double-zero) 5.3% craps (pass/come) 1.4% craps (pass/come with double odds) 0.6% blackjack - average player 2.0% blackjack - 6 decks, basic strategy* 0.5% blackjack - single deck, basic strategy* 0.0% baccarat (no tie bets) 1.2% caribbean stud* 5.2% let it ride* 3.5% three card poker* 3.4% pai gow poker (ante/play)* 2.5% slots 5% - 10% video poker* 0.5% - 3% keno (average) 27.0% *optimal strategy House advantages for major casino wagers game bet HA* baccarat banker (5% commission) 1.06% baccarat player 1.24% big six wheel average 19.84% blackjack card-counting -1.00% blackjack basic strategy 0.50% blackjack average player 2.00% blackjack poor player 4.00% caribbean stud ante 5.22% casino war basic bet 2.88% craps any craps 11.11% craps any seven 16.67% craps big 6, big 8 9.09% craps buy (any) 4.76% craps C&E 11.11% craps don't pass/don't come 1.36% craps don't pass/don't come w/1X odds 0.68% craps don't pass/don't come w/2X odds 0.45% craps don't pass/don't come w/3X odds 0.34% craps don't pass/don't come w/5X odds 0.23% craps don't pass/don't come w/10X odds 0.12% craps don't place 4 or 10 3.03% craps don't place 5 or 9 2.50% craps don't place 6 or 8 1.82% craps field (2 and 12 pay double) 5.56% craps field (2 or 12 pays triple) 2.78% craps hard 4, hard 10 11.11% craps hard 6, hard 8 9.09% craps hop bet - easy (14-1) 16.67% craps hop bet - easy (15-1) 11.11% craps hop bet - hard (29-1) 16.67% craps hop bet - hard (30-1) 13.89% craps horn bet (30-1 & 15-1) 12.50% craps horn high - any (29-1 & 14-1) 16.67% craps horn high 2, horn high 12 (30-1 & 15-1) 12.78% craps horn high 3, horn high 11 (30-1 & 15-1) 12.22% craps lay 4 or 10 2.44% craps lay 5 or 9 3.23% craps lay 6 or 8 4.00% craps pass/come 1.41% craps pass/come w/1X odds 0.85% craps pass/come w/2X odds 0.61% craps pass/come w/3X odds 0.47% craps pass/come w/5X odds 0.33% craps pass/come w/10X odds 0.18% craps place 4 or 10 6.67% craps place 5 or 9 4.00% craps place 6 or 8 1.52% craps three, eleven (14-1) 16.67% craps three, eleven (15-1) 11.11% craps two, twelve (29-1) 16.67% craps two, twelve (30-1) 13.89% keno typical 27.00% let it ride base bet 3.51% pai gow poker skilled player (non-banker) 2.54% pai gow poker average player (non-banker) 2.84% red dog basic bet (six decks) 2.80% roulette single-zero 2.70% roulette double-zero (except five-number) 5.26% roulette double-zero, five-number bet 7.89% sic bo big/small 2.78% sic bo one of a kind 7.87% sic bo 7, 14 9.72% sic bo 8, 13 12.50% sic bo 10, 11 12.50% sic bo any three of a kind 13.89% sic bo 5, 16 13.89% sic bo 4, 17 15.28% sic bo three of a kind 16.20% sic bo two-dice combination 16.67% sic bo 6, 15 16.67% sic bo two of a kind 18.52% sic bo 9, 12 18.98% slots dollar slots (good) 4.00% slots quarter slots (good) 5.00% slots dollar slots (average) 6.00% slots quarter slots (average) 8.00% sports betting bet $11 to win $10 4.55% three card poker pair plus 2.32% three card poker ante 3.37% video poker selected machines -0.50% *house advantages under typical conditions, expressed "per hand" and including ties, where appropriate. Optimal strategy assumed unless otherwise noted. Note: this summary is the intellectual property of the author and the university of nevada, las vegas. Do not use or reproduce without proper citation and permission. Cabot, anthony N., and hannum, robert C. (2002). Gaming regulation and mathematics: A marriage of necessity, john marshall law review, vol. 35, no. 3, pp. 333-358. Cabot, anthony N. (1996). Casino gaming: policy, economics, and regulation, UNLV international gaming institute, las vegas, NV. Eadington, william R., and cornelius, judy (eds.) (1999). The business of gaming: economic and management issues, institute for the study of gambling and commercial gaming, university of nevada, reno, NV. Eadington, william R., and cornelius, judy (eds.) (1992). Gambling and commercial gaming: essays in business, economics, philosophy and science, institute for the study of gambling and commercial gaming, university of nevada, reno, NV. Epstein, richard A. (1995). The theory of gambling and statistical logic, revised edition, academic press, san diego, CA. Feller, william (1968). An introduction to probability theory and its applications, 3rd ed., wiley, new york, NY. Griffin, peter A. (1999). The theory of blackjack, 6th ed., huntington press, las vegas, NV. Griffin, peter (1991). Extra stuff: gambling ramblings, huntington press, las vegas, NV. Hannum, robert C. And cabot, anthony N. (2001). Practical casino math, institute for the study of gambling & commercial gaming, university of nevada, reno. Humble, lance, and cooper, carl (1980). The world's greatest blackjack book, doubleday, new york, NY. Kilby, jim and fox, jim (1998). Casino operations management, wiley, new york, NY. Levinson, horace C. (1963). Chance, luck and statistics, dover publications, mineola, NY. Millman, martin H. (1983). "A statistical analysis of casino blackjack," american mathematical monthly, 90, pp. 431-436. Packel, edward (1981). The mathematics of games and gambling, the mathematical association of america, washington, D.C. Thorp, edward O. (1984). The mathematics of gambling, gambling times, hollywood, CA. Thorp, edward O. (1966). Beat the dealer, vintage books, new york, NY. Vancura, olaf, cornelius, judy A., and eadington, william R. (eds.) (2000). Finding the edge: mathematical analysis of casino games. Institute for the study of gambling and commercial gaming, university of nevada, reno, NV. Vancura, olaf (1996). Smart casino gambling, index publishing group, san diego, CA. Weaver, warren (1982). Lady luck: the theory of probability, dover publications, new york, NY. Wilson, allan (1970). The casino gambler's guide, harper and row, new york. Bob hannum is a professor of risk analysis & gaming at the university of denver where he teaches courses in probability, statistics, risk, and the theory of gambling. His publications includepractical casino math (co-authored with anthony N. Cabot) and numerous articles in scholarly and gaming industry journals. Hannum regularly speaks on casino mathematics to audiences around the globe. (some of this guide has been excerpted from practical casino math.) Follow unlvgaming on twitter and unlvgamingresearch on facebook © 2019 university of nevada, las vegas. Do not copy or reuse without permission. Best payout slots Games offering progressive jackpots and bonus rounds are popular with players, but slots with the best payout rates or payback percentages are considered among the top prizes in the world of gambling. After all, even a couple of extra percentage points can make a major difference when calculating the profitability of an individual slot. This article examines the definition of “payout percentage” and explains where to find the most generous slot games. While it won’t improve your actual chances of winning, the knowledge that you’re playing a more liberal slot machine should at least boost your confidence. What is a payback percentage? The payback percentage—also known as the payout percentage or return to player—is the amount of money deposited into a slot machine that is eventually paid back to the customer. This percentage is not determined in weeks or months, but rather over the life of the machine. For example, let’s say that $100,000 is inserted into a slot machine with a 92% payout percentage. According to the RTP (“return to player”), the slot should pay back $92,000 of the wager in the form of wins, while keeping the other $8,000 in profit. Keep in mind, however, that the true payout of a slot machine may take millions of spin to determine. When a machine’s software is written at the factory, this is when the payback percentage is set in accordance with local laws. For example, slots in new jersey must be set to pay back a minimum of 83%, while games in nevada have a lower limit of 75%. On average, the payout percentage for most slots ranges from 82% to 98%. Slots with a high RTP are known as “loose slots,” while their stingy counterparts are referred to as “tight slots.” since these figures are rarely reported, it’s difficult for a player to accurately determine whether the machine they’re playing is loose or tight. In previous years, the RTP was set at the factory and any additional manipulation by the casino required the software to be switched. Thanks to advances in computer technology, many casinos can now remotely manipulate the odds and payout, although they must wait until the machine has been vacant for at least four minutes (no mid-game manipulations). How to find the highest paying slot machine Casinos love to promote their slots as being loose or easy to win slot machines, but they’re tight-lipped when it comes to actually identifying the machines. In most cases, a few loosest slots are sprinkled into rows of tight machines, which still give the casino the opportunity to brag about all the loose slots they offer. Unless you happen to have a casino manager in your back pocket, it’s going to be difficult to determine a game’s true payback percentage. Gambling forums and chat rooms are often filled with people who claim to know the RTP for various machines, but you should only trust those sources with impeccable credentials. Otherwise, it’s probably an educated guess or outright lie. Games with top payback / payout percentages While it may be disappointing to hear, a so-called list of loose slot machines is useless. There are a couple of reasons for this, which I will explain below. Varies by machine – just because one slot machine from a certain series pays back 96%, another identical machine may only pay back 89%. These differences aren’t listed by the casino, so the player is left to play a guessing game. Location – even if you somehow learn that the fifth machine on the fourth row pays back 97%, it’s only a matter of time before the casino changes its physical location. When searching for the best RTP, the best strategy is to look at the minimum paybacks allowed by law. Any law-abiding casino cannot go below this number, which at least gives you a worst case scenario for the rate of return. Unfortunately, not all states have a minimum, and establishments aren’t always required to disclose their payback setting (especially indian casinos, who regulate themselves). Still, I’ve included what meager information I could gather. Arizona – 83% minimum payback Delaware – their video lottery terminals must pay between 87% and 95%. Kansas – 87% minimum (80% at indian casinos) Louisiana – casino slots must pay no less than 80% and no more than 99.9%. The minimum return at locations other than casinos is 80%, with a maximum of 94%. Maine – 89% minimum payback Maryland – 87% minimum payout Minnesota – RTP must be between 80% and 95%. Nevada – 75% minimum RTP New jersey – 83% minimum payback New mexico – between 80% and 96%, although indian casinos have a required minimum of 80%. North carolina – payout must fall between 83% and 98%. North dakota – slots carry a minimum return of 80%. West virginia – carries of minimum requirement of between 80% and 95%. Wisconsin – minimum return of 80%. Slots with the best payback percentage are highly coveted in the world of gambling, so expect a feeding frenzy whenever a game’s true RTP becomes known. This doesn’t happen very often, though, as casinos love to move machines around to keep savvy patrons guessing. Ultimately, your best chance comes from reading the rules, understanding the pay table, and keeping your expectations in check. Once you meet these requirements, you’re a lot more likely to walk away from the casino with a smile on your face. Top 10 slots with the highest RTP – play with the best odds By: cat marshall february 27, 2018 Whilst many people decide which slot to play based on the theme, special features or promotional offers, the savvy gamblers steer towards slots with the highest RTP. The house edge of online slot machines can vary widely, and it stands to reason that the lower the house edge, the better your chances of winning. Top RTP slots RTP bet limits free spins paylines rows reels jack hammer 2 97.10% £0.50 – £250 10-20 99 3 15 simsalabim 97.50% £0.25 – £125 yes 25 3 5 retro reels extreme heat 97.50% £0.30 – £112.50 up to 20 30 3 5 devil’s delight 97.60% £0.20 – £40 yes 20 3 5 kings of chicago 97.80% £0.05 – £50 up to 30 5 3 5 starmania 97.87% £0.10 – £20 10 10 3 5 blood suckers 98.00% £0.25 – £50 10 25 3 5 1429 uncharted seas 98.60% £0.10 – £100 25 50 3 5 jackpot 6000 95.10 – 98.90% £1 – £2 no 5 3 3 mega joker 99% £1 – £5 no 5 3 3 Of course, you should keep in mind that only the best slot sites to win offer high payout games from which you can take advantage. The return to player percentage of a game is measured over thousands of game rounds, and it stands to reason that the higher the RTP, the better the deal for the player. With this in mind, I have decided to create a list of the 10 online slots with the highest RTP. #10 jack hammer 2 (netent) – 97.1% RTP Jack hammer 2 is the first of many netent slots to make this top 10 list. This entertaining slot has a crime and adventure theme, captured in a comic book style. There are an impressive 99 bet lines in this game, providing plenty of opportunities to win. It also boasts a variety of interesting features that make the game exciting to play, whilst creating chances to win. The sticky win feature sees any winning symbol combinations held in place for a free re-spin, and they continue until no new wins are created. There is also a free spin feature, where you get up to 20 free plays, where all wins are doubled and extra wilds randomly land on the reels. Jack hammer 2 has a player friendly RTP of 97.1% #9 simsalabim (netent) – 97.5% RTP This magical themed slot recreates all the excitement of a magic show. The stage is set, with symbols such as a magician’s wand and top hat, a caged dove and a houdini-style chained chest. The hypnotist is wild, helping to complete winning symbol combinations. When you play simsalabim, keep your eyes peeled for 3 bunny rabbit symbols on the first 3 reels. These trigger the bonus game, where you pull rabbits from the hats to reveal cash prizes of up to 50500 coins. The slot also features a free spins round, which provides the potential for big wins thanks to the triple payouts. All these features combine to provide a great RTP of 97.5%. #8 retro reels extreme heat (microgaming) – 97.5% RTP The RTP of 97.5% is one of the highest you will find in the microgaming slots selection. Retro reels extreme heat has an old-school feel, with symbols you’d expect to see on a classic fruit machine, including cherries, lemons, bells, bars and 7’s. At the same time as providing a retro feel, it includes many features which you’d expect from a modern video slot. There is a free spin bonus, where you can get up to 20 free plays with all wins doubled. There are also wild substitutions and scatter pays. A highlight is the innovative re-spin feature. After any spin, you can choose to spin just one reel, which allows increased chances of winning. #7 devil’s delight (netent) – 97.6% RTP Unleash your inner devil in this netent video slot. Set against a fiery backdrop and tombstones, the 5 reels are filled with symbols from the underworld. Devil’s delight is packed full of exciting features that provide plenty of chances to stack up the wins. The devil wild expands to cover entire reels. Whilst the free spins bonus features win multipliers of up to x5. Yet the real highlight of the game is the unique soul reaper bonus game. Match the correct sin to each character their soul will be added to the soul-O-meter whilst you reap a coin prize. When the soul-O-meter is filled with 15 souls, the sin spins feature is activated. Here, you get 10 sin spins where you can pocket some juicy rewards. With so many cool features and a high RTP of 97.6%, this is one hell of a slot! #6 kings of chicago (netent) – 97.8% RTP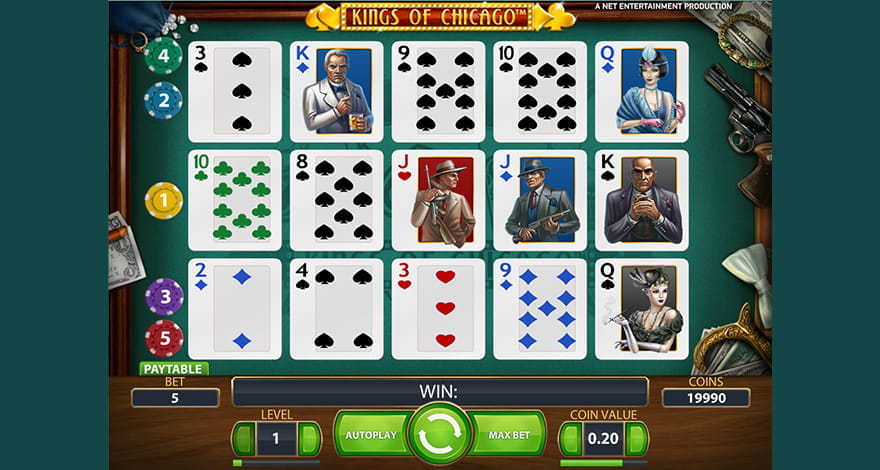 Kings of chicago mixes the best elements of a video slot with classic poker. The game is played with a deck of cards, which is shuffled before each round. Unlike normal slot machines, where payouts are made for matching symbols across paylines, in this slot, you win if you have a poker hand on one of the five paylines. The game includes a joker, which substitutes for all cards. Plus, the scatter label can randomly appear on any card. Get 3 or more and free deals, the equivalent of free spins are triggered. You can bag up to 30 free deals in the special feature and all wins are doubled. This innovative slot machine provides a unique twist on what you expect from a video slot, and boasts an impressive RTP of 97.8%. #5 starmania (nextgen) – 97.87% RTP With colourful star symbols set against a pretty outer space background and a spacey, ethereal soundtrack, this nextgen slot is a real treat for the senses. Wilds are stacked onto the reels boosting your shot at winning combinations. There is also a free games feature, where extra stacked wilds can help create some big wins. The game features 10 paylines and wins are paid in both directions. With every line win, you also have the option to gamble your prize, for a chance to double or even quadruple your win multiple times. The great graphics, exciting features and favourable RTP of 97.87% make starmania a real hit with players. #4 blood suckers (netent) – 98% RTP The vampire genre has never been more popular, and it is the inspiration for this spooky netent slot. You’ll see various blood suckers adorning the reels, along with the weapons to fight them off. It is not merely the impressive 98% RTP that draws players to this slot, but also the rich selection of special features. There are wild substitutions, scatter pays, free spins with triple payouts and a vampire slaying bonus game. Trigger the bonus and you will find yourself in an ancient burial chamber, filled with coffins. Open the coffins to slay vampires, earning coin wins with each creature you defeat. #3 1429 uncharted seas (thunderkick) – 98.6% RTP This video slot from thunderkick is visually stunning. The reels are replaced with a medieval style hand-drawn map and the symbols include a variety of sea creatures and beasts as well as sun, moon and star symbols. The slot includes a wild symbol which expands to cover entire reels, helping to create bigger wins. There is also a free spins bonus where you can earn up to 50 free goes. 1429 unchartered seas has a rewarding RTP of 98.6%, one of the highest you will find in a video slot, making it a popular choice with players. #2 jackpot 6000 (netent) – up to 98.8% RTP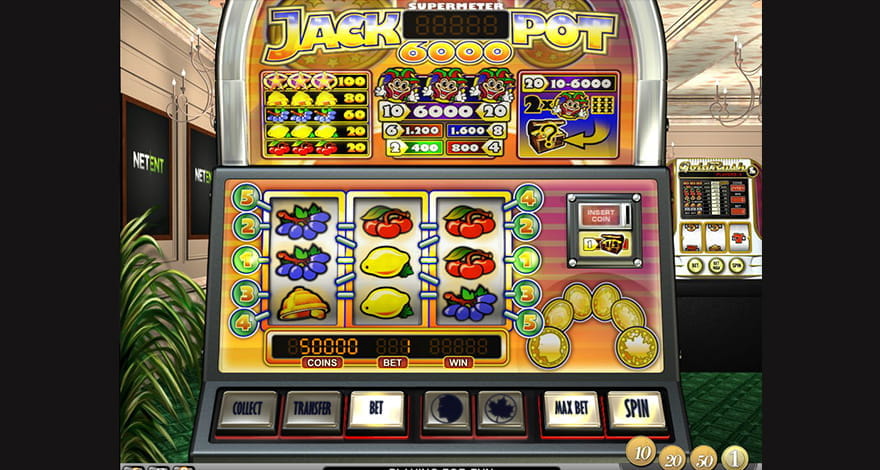 Jackpot 6000 is a thrilling classic slot machine from netent with a real old-school vibe. You can play with up to 5 paylines active, betting between 1 and 10 coins per spin. It is highly recommended to play with the maximum bet of 10 coins however, as this creates the possibility of triggering supermeter mode. In this game mode, you can win a mystery prize of between 10 – 6000 coins when just 2 joker symbols land anywhere on the reels. Also, getting 3 jokers on a payline in supermeter mode guarantees a jackpot payout of 6000 coins. When you play jackpot 6000 with 1 – 8 coins, the RTP is a paltry 74.9% – 79.2%. Yet with 10 coins in play, the RTP ranges from 95.1% – 98.9%. The variance is because supermeter mode is skill based, so you can directly impact the outcome. #1 mega joker (netent) – up to 99% RTP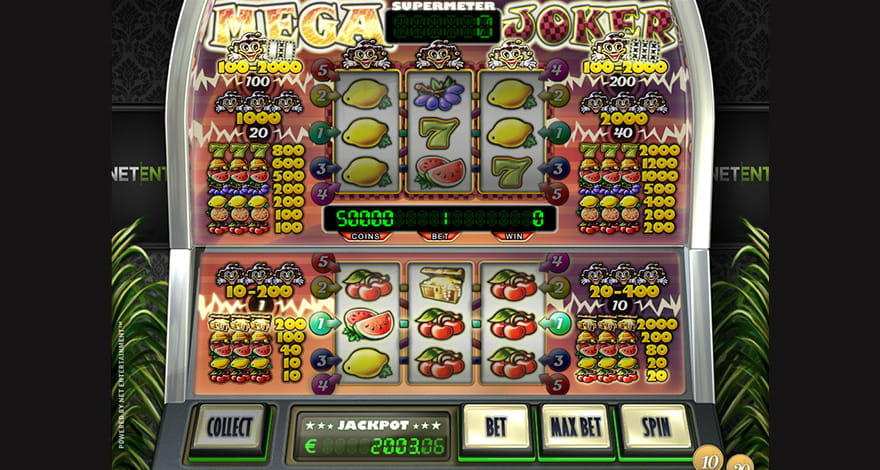 Whilst jackpot 6000 boasts an extremely high RTP, it is just beaten to the top spot by another netent classic slot; mega joker. Bet with just 1 coin and the RTP is an underwhelming 76.9%. Yet on the other hand, a max bet of 10 coins elevates the RTP to between 89.1% – 99%. Furthermore, it provides bigger payouts and the supermeter mode. In supermeter mode, you need to choose the bet level and the optimum level at which to collect your winnings. It is this element of skill which can increase the RTP. The skill component, retro style and engaging gameplay make mega joker a firm favourite with players. Frequently asked questions Because our goal is to keep you well informed we have put together a list of the most frequently asked questions and our team of experts has provided the answers below. �� what are the best paying slots? The best paying slots are the ones that feature a high RTP because that translates to a small house edge such as netent’s jack hammer 2 slot or simsalabim, with a return to player percentage of over 97%. ✍ how do I choose a good slot machine? In choosing a good slot machine a player should look for high payouts, volatility and the features of the game itself. For example, you are bound to have a higher return on your investment while playing a slot with free spins and multipliers. �� what is the average payout on slot machines? The average payout on slot machine varies among slots but you are going to find a higher return-to-player percentage in the recommended online casinos as compared to the traditional slot machines. Blood suckers slot and 1429 uncharted seas slot have a very high RTP of over 98%. �� what is a high variance slot machine? High variance slots are destined for gamblers who are willing to play for huge wins. Kings of chicago is a great example in that direction because it features not only a high RTP but also a high variance, which makes it ideal for our example. Flexible betting limits, free spins and a unique twist on slots as we know them are just a few perks of enjoying this title. Best slot machines by payout percentage Sick of playing slot machines with rubbish payouts? Join the club! To solve that exact problem we’ve put together a list of the best slots by payout percentage so you know that the machines your playing are the best they can possibly be. Top 12 online slots by RTP Click ‘play now’ buttons to visit an online casino offering the game: Top 50 slots by payouts Click name of slot machine to visit a casino offering the game: Best payout slot machines by software provider Whilst our comprehensive table of payout percentages for slot machines is undoubtedly illuminating, we have gone one step further in trying to help you find the best online slots. This graph shows the eight main software providers for online slots and the average payout percentage across all of their games. Essentially it shows you which providers apply the smallest ‘house edge’ and thus produce the best slot machines for players. RTP % by slot manufacturer There are a couple of things that really stand out when you look closely at the graph: Amaya slots are by far and away the worst slot machines for payouts with a 92% RTP average (more on that later). Netent make the most player friendly slot games averaging a 96.51% payout percentage. The majority of companies are within 1% of each other setting an online industry standard of about 95% for slot payouts. Online slots have a comparatively impressive payout percentage across the board as compared to land-based slot machines (85% average), with upwards of 90% representing a kind of industry standard. We’ve also built specific pages which breaks down the games offered by each brand: Why are amaya payouts so bad? Amaya lags quite significantly behind the others with a payout percentage of 92%… why are they so far behind the rest? Amaya are a canadian company based in montreal and after their purchase of the parent company of pokerstars and full tilt poker in 2014, became the world’s largest public listed online gambling games company. It may be therefore, that as market leaders there is less pressure on amaya to match or better their competitors’ payout percentages. Amaya have also recently purchased several other slots providers including aristrocrat and chartwell. Both companies were known for their low return to player percentages and therefore could be dragging the amaya averages down. However at the core of this issue is the fact that amaya are a major player in the creation of software for real world slot machines and as such clearly want to bring the lower land based percentages to the online scene (how very noble of them indeed). Slot machine payouts vs other casino games Plenty of useful conclusions can be drawn from simply looking at the payout percentages of different slots games and software providers. However… it is also important to look at the RTP percentages of slots as compared to other online casino games. RTP percentages: slots vs other casino games *graph assumes a player is playing the most favourable variation of the game and is employing perfect strategy. Keno is the obvious place to start when looking at this data, as its RTP percentage is significantly lower than any other at 73% (avoid at all costs folks). Blackjack has a much higher average RTP percentage of 99.50% and when played correctly is the most player friendly casino game there is. It’s pretty difficult to land a significant payday playing blackjack. You’ve got to get on a seriously hot streak which lasts a significant amount of time to make a lot of money. Slots machines, although with an average RPT of 95.67%, do offer the chance to score that big payout and it could be argued that sacrificing a bit of house edge to get that opportunity is worth it. As a side note blackjack’s very low house edge is why it’s pretty much always excluded from wagering requirements for online casino bonuses. With the bonus money added to expected returns when clearing the bonus it can actually produce an edge for the player if perfect strategy is employed. How do RTP percentages work? RTP or payout percentages are a representation of the average rate at which a game – be it slots or otherwise – pays out to players, as compared to the total amount that players stake. In general, online slots games have a payout percentage of around 95% and in the simplest possible terms this means that on average the game will pay out £95 for every £100 staked on it. That does not mean that every player is guaranteed £95 worth of payout if and when they stake £100 however, as the percentages are based upon a very high number of spins. General probability and more simply the law of averages, means that an individual player could still win far more than they stake or lose considerably more than 5% in one session or over an extended period of time. What it does mean is that on average the online casino or game provider will take 5% of the money staked on the game for themselves, and that is called the ‘house edge’. How are slot machine payouts calculated? For players… RTP = (total amount returned to players) / (total amount bet by players). That calculation will always return the result in the form of a decimal (e.G. 0.95) and it can then simply be translated into a percentage, which in that example would be 95%. For the casinos… the number of symbols built into the game, the amount of combinations of those symbols which provide a payout, the value of those payouts and the probability of those combinations occurring combine to produce the games overall RTP %. Why do slots have different payouts? Online slot games software providers have no real restrictions placed upon them in terms of the initial RTP percentage they build into their games. The UK gambling commission nor any other regulatory body of note impose a statutory minimum upon online slots games and as such the providers can set the level themselves. Levels are determined by the paytable and symbols in the game, these differ from game to game and therefore payouts differ as well. They are set to make machines attractive to players whilst still providing a house edge for the casino. The best slots from a players point of view are usually always those with the highest possible payout percentages. Do online slots or land based have better payouts? The best slot machine games, where payouts are concerned, are always online based. The percentage falls dramatically live as compared with online. Where the general online average RTP percentage tends to hover around 95%, land based casinos can – and often do – offer percentages as low as 75%. That figure in fact, is one which is often linked to machines in las vegas where the state imposed minimum is indeed only 75%. Other global regulatory bodies however, do impose a more stringent minimum on physical slot machines, with the state of new jersey requiring 83% and the state of mississippi 80% for example. In the UK meanwhile, the UK gambling commission does not actually impose any statutory minimum. It does dictate however, that all machines must display their RTP percentages clearly to players and that does tend to prevent casinos and bookmakers from allowing the percentages to fall too low as to make games unfair. Can casinos change payout percentages? The answer to this question tends to be no, but the explanation of that answer differs in terms of live and online slots games. Online casinos To deal with online games first, as we have mentioned online there is no statutory minimum RTP percentage which allows providers to set their own levels. What they cannot do however, is to routinely alter or skew those percentages or to lie about them to their customers. This is prevented by the necessity of online slots providers to have their games regularly tested by independent testing boards. These boards must themselves by licensed by the relevant legislative bodies and will check that a provider’s games generate random combinations, are not biased towards or away from certain combinations and deliver the RTP percentage that they claim. If you stick to online gaming sites which are legit and registered with testing boards such as ecogra in the UK, itech labs in australia or gaming laboratories international in the USA therefore, you can be sure that the games have fair and consistent RTP percentages. Live casinos With physical slot machines, the payout percentage tends to be set when the imbedded software is originally written and as such can only be altered by the physical switching of the software or firmware. That is a time consuming and difficult process, and is one that is also often subject to different rules according to the jurisdiction in which the machine is operated. In the US state of new jersey for example, each machine is fitted with a tamper proof seal to ensure that any switch of software can only be carried out in the presence of a gaming control board official. All of that, together with the fact that it is an almost universally applied rule that the RTP percentage for a machine must be clearly displayed to players, makes it very difficult therefore for casinos and other slots providers to change percentages whenever they want. But essentially in a live environment it can be done, it’s just quite difficult to do it. Casino stats: why gamblers rarely win In a down economy, it's normal to start thinking of alternative ways to generate some extra money, but if you're tempted into thinking gambling is one of those good alternatives, you need to keep reading. Once you step foot into a casino and exchange your money for chips, you've sold away your only advantage, which is staying out of the casino to begin with. Casinos can bring great shows, food and entertainment, but statistically they won't bring you much more than that. (for more, see going all-in: comparing investing and gambling.) IN PICTURES: 7 forehead-slapping stock blunders Big business and big profits to say casino gambling is a lucrative business would be an understatement. Last year, commercial casinos brought in a gross revenue of about $31 billion and indian casinos cashed in for about $26 billion. Although revenue from private casinos was down last year, it was still three-times higher than hollywood's 2009 ticket sales revenue of $10.6 billion, a banner year for the silver screen. It's no surprise where those profits are coming from, but that didn't stop over 36 million visitors from showing up in las vegas last year alone, with some hoping to win more money than they came in with. Games of no chance math is the universal language, and it rarely ever lies. Each game you play at a casino has a statistical probability against you winning. Every single time. This house advantage varies for each game, and helps ensure that over time the casino won't lose money against gamblers. For people who are really good at blackjack, the advantage for the casino might only be 0.5%, but certain types of slot machines might have a 35% edge over a player, and other games fall somewhere in between. The slot machine odds are some of the worst, ranging from a one in 5,000 to a one in about 34 million chance of winning the top prize when using the maximum coin play. (read more, in are you investing or gambling?) The house advantage obviously doesn't mean that you can't win, because people do and sometimes they win substantial amounts, but it does mean that the more you play, the more the math works against you and the better the chances are of you walking out of the casino with less money in your wallet than when you came in. Everyone's (not) a winner think of all those profits we mentioned earlier as all of the losses from casino patrons each year. Of course, some of the money may come from other venues within the casino, but the breadwinner for this industry is the games. Now, think of yourself walking into a casino with the feeling that you're going to beat those odds (or profits) because luck, whatever that is, is on your side. Not likely. You can't even bet on winning or losing streaks either. If you'd had a slew of bad hands, the likelihood of that turning into a winning streak simply doesn't exist, it's not in the cards, or math for that matter. The betting rip current aside from the entertainment of casinos, some people do get swept into an addiction that far surpasses the entertainment value of the games. Only a small percentage of gamblers, about 5%, reach that point, but unfortunately it's estimated that their losses make up a quarter of the profits for the casinos. This is all the more reason to understand the house advantage and how it works against a player who has lost a significant sum and is spending lots of time in the casino trying to win it back. The more a player struggles to get ahead, the more he gets pulled into additional losses. (read more background info, in sinful investing: is it for you?) Quit while you're ahead almost every time, it's in your best financial interest not to walk into that casino and place the bet - the math simply isn't your friend. For those who want to press their luck anyway, make sure to quit while you're ahead, because that winning streak you're on is definitely all in your head. (looking for more action? Check out A quick and dirty look at sports gambling.) An analysis of slot machine payback percentages at seminole casinos in florida By steve bourie The seminole tribe of florida has six casinos in the state: seminole hard rock hotel & casino-tampa; seminole hard rock hotel & casino-hollywood; seminole casino-coconut creek; seminole classic casino-hollywood; seminole casino-brighton; and seminole casino-immokalee. All of their casinos offer slot machines and five of them also offer blackjack, as well as other kinds of house-banked card games. According to the miami herald, it was estimated those casinos generated about $2.3 billion in profits in 2016 http://www.Miamiherald.Com/entertainment/article166085722.Html. Since the average U.S. Casino generates about 65% of its profits from its electronic gaming machines, it would be fair to estimate that the tribe’s machines earn about $1.5 billion a year for them. The only other competition for the tribe’s casinos are the eight local pari-mutuels in miami-dade and broward counties which all offer slot machines, but are not allowed to offer live table games, such as blackjack. All of these pari-mutuel casinos, also known as racinos, are in competition with the seminole’s three broward county casinos, but the seminole hard rock hotel & casino in hollywood alone generates more profits than all eight of the racinos combined. Florida gaming regulations require all of the pari-mutuel casinos to report how much their slot machines actually pay back to the public. This “average payout percentage” information is available to the public and can be seen on the state’s website at http://www.Myfloridalicense.Com/dbpr/pmw in the “slot revenues” section. Additionally, each racino must post a sign in the casino showing the average monthly payback percentage for all of their gaming machines. Usually, the average for all of the casinos is around 92.5% The seminoles are not required to release information on the payout percentages for any of their casinos and they keep this information a closely guarded secret. They say that their machines pay out at a rate comparable to the pari-mutuels, but no one knows for sure, and the topic is sometimes a source of controversy. If you read reviews of seminole casinos on yelp, tripadvisor, or on our website at americancasinoguide.Com you will see some reviewers say they believe the machines are set to around 60%, or lower. As someone who has written about casino gambling for more than 25 years, I know that isn’t true. The procedure for deciding what a slot machine is set to pay back to the public is rather simple. When a casino orders a slot machine the manufacturer will offer them a choice of chips to put in the machine and that chip is what controls the long-term payback percentage in that machine. Generally, there are about six to eight different chips to choose from and the payback percentages can be as high as 98 percent to as low as 82 percent. Casinos, almost universally, put the highest-paying chips in the highest denomination machines and the lowest-paying chips in the lowest denomination machines. This means that $25 slots will have chips returning around 95-98 percent and the penny machines will have chips returning around 86-89 percent. The lowest payback I ever heard of for a chip was about 80 percent, so I knew that the 60 percent number in the user reviews was not correct, but could there be some way to find out what the machines at the seminole casinos really paid back to the public? After a lot of research, I believe that I have correctly calculated this information and what follows is my story of how I did it, plus a simple formula to show how anyone can do it. Additionally, we’ll take a look at the returns on some specific machines at some seminole casinos and see how they compare to the returns at other casinos. Now, in order to start this discussion properly, you’ll first need some background information on how casinos work. When discussing how casinos make money, it is important to know the term “theo,” which is short for theoretical. This is how a casino expects to make money on its games. It’s referred to as “theo” because it is a theoretical number that is not guaranteed. However, the casino knows that the longer you play, the more likely your loss will approach the theoretical win for that particular game. As an example, if you play a slot machine that has a 10% theo, then the casino would expect to keep about 10% of all the money you play through that machine. So, if you played $1,000 through that slot machine, the casino would calculate its theoretical win as $100 because 10% of $1,000 is $100. Now, since this is gambling, anything can happen when you play that machine. You may win $600, or you may lose $400 and, actually, the casino itself doesn’t know what will happen. All they know is that as long as people continue to play that machine, the casino will end up keeping about 10% of the money that goes through that machine because the machine has a “theo” of 10%. In order for a casino to calculate your total theo for your visit, and what you are worth as a player to them, your play must be tracked and that is done by the player’s club at each casino. All casinos have a player’s club where visitors can join and have their play tracked on the machines in order to earn “comps” such as free food, free drinks, free shows, free gifts, invitations to special events and more. To track your play you are issued a card, similar to a magnetic-striped credit card, that is inserted into the machine and it will track your wins and losses, as well as the total amount of all your bets. Naturally, the more you play on the machines, the more free stuff you will get from the casino. When deciding how much to give you back in benefits for your play, the casino must first calculate your total theoretical loss to determine how much they have earned from you. Then, based on that total, they will rebate a certain percentage back to you in the form of comps and free play. The actual percentage rebated to the player is a trade secret for each casino but, again, it is always based on a player’s tracked theoretical loss. I live only one mile from the seminole hard rock casino in hollywood and I joined their seminole wild card player’s club shortly after the property opened in 2004. Although I did not play much in the ensuing years, in late 2013 I began to play rather heavily and it continued through early 2017. My game of choice was video poker rather than slot machines because there is a skill involved in video poker and I used software to learn how to play my hands properly. Eventually, I played at an expert level that allowed the casino to have only a slight mathematical edge over me. Overall, my results were pretty good as I hit quite a few royal flushes in 2016 and that helped me to come out ahead for my three years of play. In early 2017 the casino made some changes to their video poker games, which made them less desirable, and I stopped playing. During my period of play I used that opportunity to analyze the seminole wild card player’s club and, following, is what I discovered. The set-up of the seminole wild card player’s club is somewhat unusual because at most casinos when you play a machine you will earn points based on the total amount of money you put through a machine. On some machines it may be that $5 earns one point, while on other machines it may be $10 or $25 earns one point. Try an online casino for FREE. We have over 15 no deposit bonus codes. No credit card needed, just sign up and start playing! The seminole wild card player’s club is different because players don’t earn points on each machine, instead they earn comp dollars. As an example, for playing $10 through one machine you might earn six cents, while on another machine you might only earn three cents. So, if you ended up playing $1,000 for the day on the same machine, your comps would total $6 on the first machine, or $3 on the second machine. As a player, you wouldn't really know why one machine gave more comps, but you could correctly theorize that the machines that had a higher rate meant that the casino was making more of a theoretical win from you and that's why they could give you back more comps. The comps you earned could then be spent like regular dollars at hotels, restaurants, bars, lounges and retail stores at any of the six seminole casinos. Besides earning comps, each day's play also earned you status credits and those enabled you to reach a higher player's card level. Interestingly, there was no information on a formula for how the status credits were earned. As a player all you knew was that you could check your account each day to see how many status credits you earned for your previous day's play. The player's club only has three tiers: platinum, elite and X card. All players start at platinum and to reach elite you need to earn 3,750 status credits within a three-month period. X card is reserved for the casino's biggest players, but there is no public information available on what is needed to attain that level. I easily attained elite level and after tracking the comps and status credits I earned each day, within a few months I began to realize that the status credits actually represented my total theoretical loss for each day. I was able to confirm this through test play on certain machines, as well as speaking with other knowledgeable players. Once I knew that the earned status credits represented my total theoretical loss I was then able to compare that number to the total comps I earned on that same day and I realized that there was a relationship between those two numbers. As an example, one day I earned $48.75 in comps and I was awarded 828 status credits. By multiplying $48.75 by a factor of 17 the result was 828. Another day I earned $30.83 in comps and 524 status credits. Once again, by multiplying $30.83 by 17 the result was 524. That relationship was absolute and no matter what day I played, I found that I could always multiply the amount of my earned comps by 17 to determine my status credits (theoretical loss) for that day. Since I now knew how to calculate my theoretical loss for the day, based on the comps I earned, I then realized that I would be able to calculate what the casino had set as its theoretical payback percentage for any electronic game on the floor. How to calculate the theoretical payback percentage on a slot machine - I believe that anyone can calculate the theoretical payback percentage on any gaming machine in a seminole casino by using a formula that I created. The key to calculating a machine’s theoretical payback percentage is to track how many comp dollars you earn for putting exactly $100 in play through a machine. For example, if you bet $1 a spin, just track how many comp dollars you have earned after making 100 bets. Once you know that number, you can simply multiply it by 17 and you will know the casino’s theoretical win rate for that machine. Deduct that number from 100, and you will then know the theoretical payback for that machine. As an example, let’s say you put $100 through a penny slot machine and you earn 54 cents in comps. Just multiply .54 x 17 and you will get 9.18, which represents the casino’s theoretical win rate for that machine - 9.18%. Then, deduct 9.18 from 100 and you get 90.82 which would represent the casino’s theoretical payback percentage for that particular machine - 90.82%. I found this method to be accurate and I tested it on dozens of machines at four different seminole casinos. It should also work at the other two seminole casinos since they all share the same player’s club. One word of warning, however, is that I found the method to only be accurate for single-denomination machines. If you play a multi-denomination machine the method cannot be relied upon to give you an accurate payback percentage for all of the denominations. How do slot paybacks at the hard rock in hollywood compare to the other local casinos? In trying to determine an average payback percentage for slot machines at the hard rock in hollywood, I realized that it would not be possible to get an actual accounting and I would just have to make an educated guess based on the results of playing some machines in different denominations. Therefore, I randomly played 10 different machines throughout the casino in three different denominations: pennies, quarter and dollars. As mentioned previously, I had to play exactly $100 through each machine and in some instances it wasn’t possible to play exactly $100, so I might have gone over by a few pennies. In the table below you can see the results for playing 10 random penny slots and the average theoretical return was 88.37% Slot machine software RTP% monopoly big event barcrest Date played machine # name comps earned for $100 coin-in theoretical hold theoretical payback 30-nov 012714 10130 moon maidens $0.68 11.56% 88.44% 17-aug 040312 04892 quick strike mystery rewards 0.69 11.73% 88.27% 30-nov 010103 11114 desert dawn 0.59 10.03% 89.97% 17-aug 034106 09083 quick hit platinum 0.64 10.88% 89.12% 17-aug 050907 10010 fu dao le 0.69 11.73% 88.27% 30-nov 012106 11952 jungle riches 0.69 11.73% 88.27% 17-aug 013504 10609 super wheel blast lion of venice 0.70 11.90% 88.10% 17-aug 013510 10618 wild leprecoins 0.70 11.90% 88.10% 17-aug 043702 08245 buffalo special edition 0.72 12.24% 87.76% 14-oct 051502 12178 rumble rumble B ison 0.74 12.58% 87.42% average 11.63% 88.37% In the table below you can see the results for playing 10 random quarter slots and the average theoretical return was 90.89% Date play ed machine # name comps earned for $100 coin-in theoretical hold theoretical payback 30-nov 067510 11231 the enforcer $0.45 7.65% 92.35% 30-nov 032301 32091 triple double diamond 0.53 9.01% 90.99% 30-nov 013704 09830 thunder eyes 0.54 9.18% 90.82% 30-nov 074701 11731 quick hit platnum plus 0.63 10.71% 89.29% 30-nov 101406 08598 cash cove 0.49 8.33% 91.67% 16-oct 064103 09534 colossal cash grand dragon 0.47 7.99% 92.01% 16-oct 034708 12048 double hot fire 0.54 9.18% 90.82% 16-oct 075307 10059 black diamond 0.59 10.03% 89.97% 16-oct 101309 09950 mystery rewards glistening jade - rapid hit fever 0.53 9.01% 90.99% 30-nov 075305 09528 crystal star 0.59 10.03% 89.97% average: 9.11% 90.89% In the table below you can see the results for playing 10 random dollar slots and the average theoretical return was 91.40% Date play ed machine # name comps earned for $100 coin-in theoretical hold hold theoretical payback 17-aug 075504 50787 spin & win instant spin $0.47 7.99% 92.01% 17-aug 069001 09079 quick hit platinum 0.51 8.67% 91.33% 12-oct 069710 09348 wild red sevens 0.44 7.48% 92.52% 12-oct 069707 09345 triple 777 red hot 3 reels 0.44 7.48% 92.52% 12-oct 041806 05563 black & white 7s 0.47 7.99% 92.01% 30-nov 067804 10546 double jackpot lions share 0.59 10.03% 89.97% 14-oct 065405 10508 midnight eclipse 0.47 7.99% 92.01% 30-nov 068904 08728 dragons luck 0.59 10.03% 89.97% 30-nov 068105 10158 sky rider 0.58 9.86% 90.14% 16-oct 055307 50806 blazing 7s 3 reel 0.50 8.50% 91.50% average: 8.60% 91.40% So, now that we have analyzed the theoretical payback percentages on these machines, how do they compare to the actual returns on slots at other south florida casinos in those same denominations? Well, unfortunately, florida’s division of pari-mutuel wagering, which compiles the statistics on payback percentages for all racetrack casinos only releases information on the average payout for all machines within each casino and not for specific denominations. We did put in a public records request asking for a breakdown of those stats by denomination, but we received the following reply: “the division does not maintain information responsive to the following request: slot machine gaming revenue reports by denomination (one cent, nickel, quarter, dollar, etc.).” Since we couldn’t get information on payback percentages by denomination, it was not possible to compare the hard rock’s machines with those at the pari-mutuels. However, it was possible to make an educated guess about the overall returns on the hard rock’s machines. For the 12-month period from july 2016 through june 2017, the pari-mutuel casino with the highest average returns was magic city at 93.55% and the lowest returns could be found at the isle in pompano where they averaged 90.91%. Therefore, based on the numbers shown in the tables above, I would have to agree that the hard rock hollywood’s slot paybacks are “comparable” to those at other local casinos and they are not set to pay back at the low rates that some people would suggest. How do returns on machines at the seminole hard rock casino in tampa compare to returns at casinos in south florida? On the american casino guide website visitors can leave a review for any U.S. Casino and the seminole hard rock in tampa has gotten almost 200 reviews - https://www.Americancasinoguide.Com/florida/seminole-hard-rock-hotel-a-casino-tampa.Html the vast majority of those reviews are complaints about how bad the paybacks are on the slot machines. The thinking seems to be that, once again, the machines are set to pay back at a very low rate, especially since the tampa casino has no competition because the nearest non-seminole casino is about 250 miles away. That sentiment seemed somewhat logical to me so I thought I would investigate further by making a trip to tampa to visit the casino. I arrived late in the day and I spent a few hours that evening, as well as a few more hours the next morning testing various machines using my formula. My thought was to find some of the exact same machines I played at the hard rock in hollywood and to see if the theoretical payback percentages were lower. This turned out to be harder than I expected as I found it difficult to find the same machines in the same denominations. One other thing I noticed was that there did not seem to be too many penny slots. Instead, the vast majority of the lower denomination games were two-cent slots. This was not the case at the hard rock casino in hollywood, where penny machines were abundant. Eventually, I did find a few machines, in three specific denominations, that were the exact same as the ones I played in hollywood and the table below shows how the results compared. For penny games there were three machines I tested and, interestingly, all three had the same theoretical payback percentage as at the hollywood hard rock. Date played machine # name comps earned for $100 coin-in theoretical hold theoretical payback location 14-oct 051502 12178 bison rumble rumble $ 0.74 12.58% 87.42% hollywood 23-oct 082802 05797 bison rumble rumble $ 0.74 12.58% 87.42% tampa 17-aug 050907 10010 fu dao le $ 0.69 11.73% 88.27% hollywood 23-oct 092206 6026 fu dao le $ 0.69 11.73% 88.27% tampa 17-aug 070712 04056 buffalo special edition $ 0.72 12.24% 87.76% hollywood 23-oct 043702 08245 buffalo special edition $ 0.72 12.24% 87.76% tampa Finding quarter games proved to be a bit harder. I only found two machines that were identical to ones at the hollywood casino and, once again, the theoretical payback percentages matched up for both casinos. Date played machine # name comps earned for $100 coin-in theoretical hold theoretical payback location 16-oct 075307 10059 black diamond $ 0.59 10.03% 89.97% hollywood 23-oct 324002 30380 black diamond $ 0.59 10.03% 89.97% tampa 30-nov 075305 09528 crystal star $ 0.59 10.03% 89.97% hollywood 23-oct 015205 30371 crystal star $ 0.59 10.03% 89.97% tampa At the dollar level I found four machines that matched up with their hollywood casino counterparts. On the first one, triple 777 red hot three reels, the comps earned were the same as at the hollywood casino. This was great because the comp rate on every machine was matching up perfectly, so far, but that soon stopped. Date played machine # name comps earned for $100 coin-in theoretical hold theoretical payback location 17-aug 069707 09345 triple 7 red hot three reels $ 0.44 7.48% 92.52% hollywood 23-oct 380605 50232 triple 7 red hot three reels $ 0.44 7.48% 92.52% tampa 16-oct 055307 50806 blazing 7s three reel $ 0.50 8.50% 91.50% hollywood 23-oct 040111 50330 blazing 7s three reel $ 0.39 6.63% 93.37% tampa 17-aug 069001 09079 quick hit platinum $ 0.51 8.67% 91.33% hollywood 23-oct 180209 50437 quick hit platinum $ 0.41 6.97% 93.03% tampa 17-aug 075504 50787 spin and win instant spin $ 0.47 7.99% 92.01% hollywood 23-oct 353601 50197 spin and win instant spin $ 0.56 9.52% 90.48% tampa On the three-reel blazing 7’s machine the comp rate was 39 cents, which would correspond to a theoretical payback percentage of 93.37%, which was higher than the 91.50% figure for the same machine in hollywood. A similar thing happened with the next machine I tested: quick hit platinum. The comp rate on this game was 41 cents which would equal a theoretical payback percentage of 93.03% which, again, was higher than the 91.33% figure for the same machine in hollywood. Then, on the last dollar machine I played, spin & win instant spin, the results were slightly worse. That machine gave 56 cents in comps, which would correspond to a theoretical return of 90.48%, versus the same machine in hollywood which came in at 92.01% So, interestingly, the theoretical payback percentages for the first eight slot machines in tampa were either equal to, or better than, the same machines in hollywood. This was very surprising as I thought they would be lower at the tampa casino because they had no direct competition. But what about all those player reviews complaining that the slots in tampa paid less than the slots in hollywood? Well, my research showed that the machines were set to pay back at about the same rate in both places. However, there didn’t seem to be quite as many penny machines in tampa, most of them were 2-cents and higher, and this could offer an explanation. Penny machines are the most common denomination found in U.S. Casinos. For example, at the two indian casinos in connecticut, foxwoods and mohegan sun, penny machines make up about 60% of all the slots on the floor. While I didn’t take an inventory of all the machines in tampa I was struck by the fact that penny machines were not in abundance. Since the tampa casino has no competition, it could be that they were forcing players to make a higher average bet simply by having fewer penny machines available. If so, a higher average bet would result in players losing their money faster, thus explaining the sour sentiments of some players. Keep in mind that the hollywood casino would not be able to easily do the same thing because of competition from other casinos. If a player in hollywood didn’t think there were enough penny games available they could just go to a different casino. A player in tampa would not have that option. Now, looking back, it is true that one slot machine in tampa did come in with a lower theoretical rate, but that could have simply been a mistake. Keep in mind that the casino knows what the chip in each machine is set to pay back to the public on a long-term basis and, in turn, they will set the player’s club comp rate to approximate that number. Sometimes mistakes are made and the rate could be set too high, or too low. That could be what happened here, or perhaps it was intentional and there was a specific reason for that particular setting. In conclusion, I hope that everyone reading this report understands that it is not a complete analysis of all machines at either casino. To undertake such a project would have required a huge amount of manpower, plus a rather large bankroll to withstand the gambling losses that would be expected. I am just one person who set out to investigate this subject as it is my area of expertise. I have been writing about payback percentages at casinos for more than 25 years and I believe that my work is accurate. Should anyone from seminole casino operations want to present any further information on this subject I would welcome hearing from them. I would be also be glad to print any rebuttal that they might want to send to me concerning this article. So, let's see, what we have: what are the odds? - slot machine odds depend on how the virtual reel is set up. Learn about payback percentages, payout schemes and slot machine odds of hitting the jackpot. At casino slot machine winning percentage Subscribe to: Post Comments (Atom) Map of the site Post archive ►  2017 (125) ►  February (3) ►  March (11) ►  April (13) ►  May (13) ►  June (11) ►  July (12) ►  August (14) ►  September (12) ►  October (13) ►  November (12) ►  December (11) ▼  2018 (144) ►  January (11) ►  February (10) ►  March (11) ►  April (12) ▼  May (13) Tragamonedas online y juegos de casino gratis, cas... Play Video Slots Casino Online - Get 11 Free Spins... Play slots online with Grosvenor Casinos, casino s... Slot Machine, casino slot machine for sale. Find a Casino with Slot Machines NEAR ME, casino s... Study Shows Sounds Draw You to Slot Machine Games,... How Slot Machines Work, casino slot machine winnin... Novomatic Slot Machines, casino slot novomatic. Slots at Slot Boss, casino slot online. Your Top Guide to Free Slots in 2020, casino slot ... Casino slot operations Slot Oyna, casino slot oyna. Superb Slots at Spin Palace, casino slot palace. ►  June (10) ►  July (13) ►  August (12) ►  September (14) ►  October (12) ►  November (13) ►  December (13) ►  2019 (143) ►  January (10) ►  February (11) ►  March (12) ►  April (11) ►  May (13) ►  June (12) ►  July (12) ►  August (12) ►  September (13) ►  October (13) ►  November (12) ►  December (12) ►  2020 (59) ►  January (12) ►  February (9) ►  March (1) ►  April (4) ►  May (4) ►  June (4) ►  July (5) ►  August (5) ►  September (2) ►  October (5) ►  November (3) ►  December (5) ►  2021 (34) ►  January (2) ►  February (4) ►  March (5) ►  April (3) ►  May (4) ►  June (5) ►  July (3) ►  August (4) ►  September (4) My rank of online casinos for play on real money. Powered by Blogger.